Improving Deep Neural Networks (week2) - Optimization Algorithm

blairchen

data-science

Publish：Jul 21, 2018

views

Mini-batch、指数加权平均-偏差修正、Momentum、RMSprop、Adam、学习率衰减、局部最优

这节课每一节的知识点都很重要，所以本次笔记几乎涵盖了全部小视频课程的记录

1. Mini-batch

随机梯度下降法的一大缺点是, 你会失去所有向量化带给你的加速，因为一次性只处理了一个样本，这样效率过于低下, 所以实践中最好 选择不大不小 的 Mini-batch 尺寸. 实际上学习率达到最快，你会发现2个好处，你得到了大量向量化，另一方面 你不需要等待整个训练集被处理完，你就可以开始进行后续工作.

它不会总朝着最小值靠近，但它比随机梯度下降要更持续地靠近最小值的方向. 它也不一定在很小的范围内收敛，如出现这个问题，你可以减小 学习率.

样本集比较小，就没必要使用 mini-batch.

经验值 ： 如果 m <= 2000, 可以使用 batch， 不然样本数目 m 较大，一般 mini-batch 大小设置为 64 or 128 or… or 512…

算法初步

对整个训练集进行梯度下降法的时候，我们必须处理整个训练数据集，然后才能进行一步梯度下降，即每一步梯度下降法需要对整个训练集进行一次处理，如果训练数据集很大的时候，如有 500万 或 5000万 的训练数据，处理速度就会比较慢。

但是如果每次处理训练数据的一部分即进行梯度下降法，则我们的算法速度会执行的更快。而处理的这些一小部分训练子集即称为 Mini-batch。

如图，以 1000 为单位，将数据划分，令 $x^{\\{1\\}}=\\{x^{(1)},x^{(2)}……x^{(1000)}\\}$, 一般用 $x^{ \\{ t \\} }$, $y^{ \\{t\\} }$ 表示划分后的 mini-batch.

注意区分该系列教学视频的符号标记：

• 小括号() 表示具体的某一个元素，指一个具体的值，例如 $x^{(i)}$
• 中括号[] 表示神经网络中的某一层, 例如 $Z^{[l]}$
• 大括号{} 表示将数据细分后的一个集合, 例如 $x^{\\{1\\}} = \\{x^{(1)},x^{(2)}……x^{(1000)}\\}$

算法核心

假设我们有 5,000,000 个数据，每 1000 作为一个集合，计入上面所提到的 $x^{\\{1\\}}=\\{x^{(1)},x^{(2)}……x^{(5000)}\\},……$

1. 需要迭代运行 5000次 神经网络运算.
2. 每一次迭代其实与之前笔记中所提到的计算过程一样，首先是前向传播，但是每次计算的数量是 1000.
3. 计算损失函数，如果有 Regularization ，则记得加上 Regularization Item
4. Backward propagation

注意，mini-batch 相比于之前一次性计算所有数据不仅速度快，而且反向传播需要计算 5000次，所以效果也更好.

epoch

• 对于普通的梯度下降法，一个 epoch 只能进行一次梯度下降；
• 对于 Mini-batch 梯度下降法，一个 epoch 可以进行 Mini-batch 的个数次梯度下降;

epoch : 当一个完整的数据集通过了神经网络一次并且返回了一次，这个过程称为一个 epoch。

比如对于一个有 2000 个训练样本的数据集。将 2000 个样本分成大小为 500 的 batch，那么完成一个 epoch 需要 4 个 iteration。

不同 size 大小的比较

普通的 batch 梯度下降法 和 Mini-batch梯度下降法 代价函数的变化趋势，如下图所示：

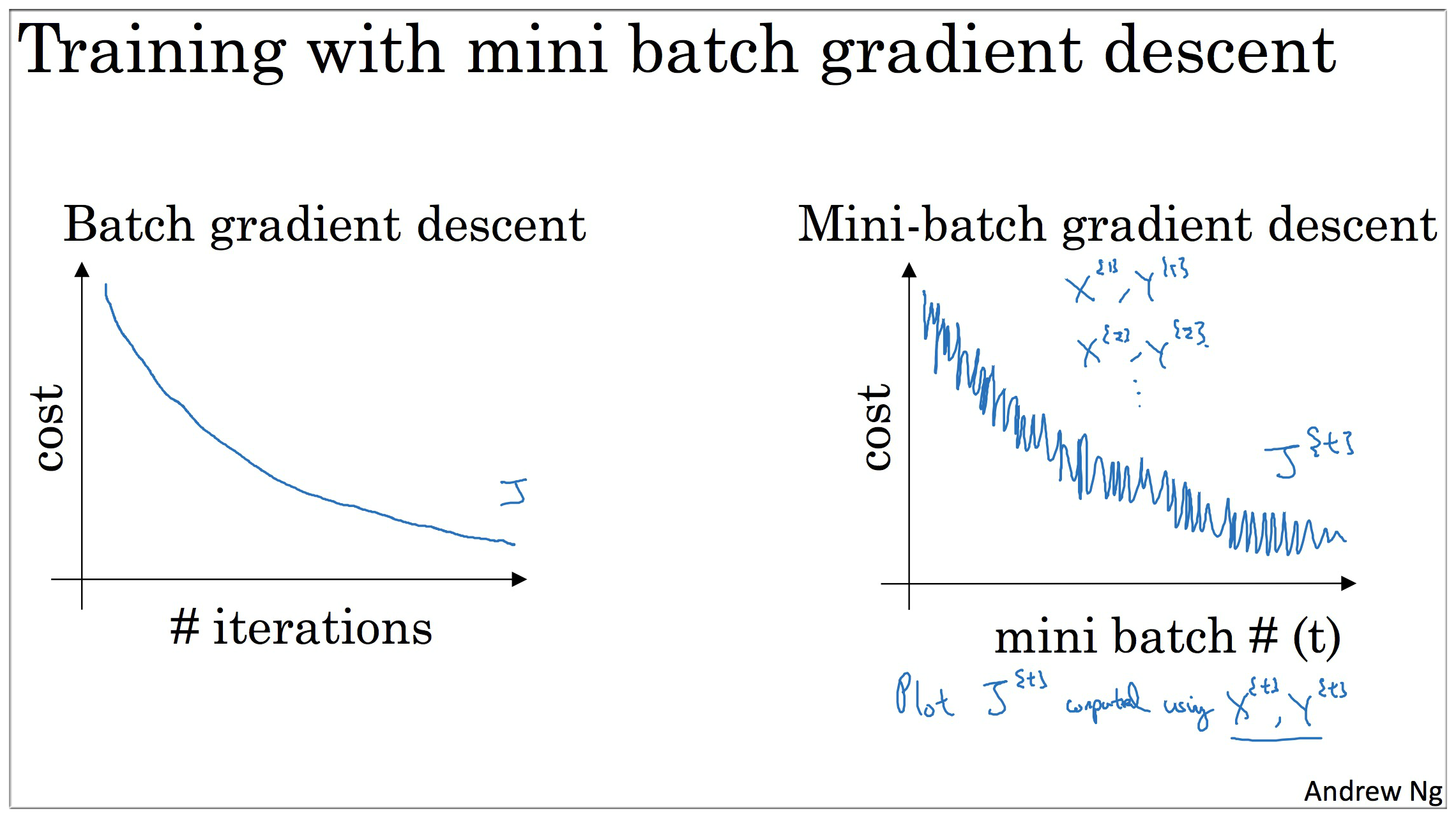
Batch梯度下降 （如下图中蓝色）:

• 对所有 m 个训练样本执行一次梯度下降，每一次迭代时间较长；
• Cost function 总是向减小的方向下降。

说明: mini-batch size = m，此时即为 Batch gradient descent $(x^{\{t\}},y^{\{t\}})=(X,Y)$

随机梯度下降 （如下图中紫色）:

-对每一个训练样本执行一次梯度下降，但是丢失了向量化带来的计算加速；

• Cost function 总体的趋势向最小值的方向下降，但是无法到达全局最小值点，呈现波动的形式.

说明: mini-batch size = 1，此时即为 Stochastic gradient descent $(x^{\\{t\\}},y^{\\{t\\}})=(x^{(i)},y^{(i)})$

Mini-batch梯度下降 （如下图中绿色）:

• 选一个 $1<size<m$ 的合适的 size 进行 Mini-batch 梯度下降，可实现快速学习，也应用了向量化带来的好处
• Cost function 的下降处于前两者之间

Mini-batch 大小的选择

• 如果训练样本的大小比较小时，如 $m⩽2000$ 时 — 选择 batch 梯度下降法；
• 如果训练样本的大小比较大时，典型的大小为：$2^{6}、2^{7}、\cdots、2^{10}$
• Mini-batch 的大小要符合 CPU/GPU 内存， 运算起来会更快一些.

2. Exponentially weighted averages

为了理解后面会提到的各种优化算法，我们需要用到指数加权平均，在统计学中也叫做指数加权移动平均.

指数加权平均的关键函数：

$v\_{t} = \beta v\_{t-1}+(1-\beta)\theta\_{t}$

首先我们假设有一年的温度数据，如下图所示

我们现在需要计算出一个温度趋势曲线，计算方法(指数加权平均实现)如下：

$v\_{0} =0 \\\\ v\_{1}= \beta v\_{0}+(1-\beta)\theta\_{1} \\\\ v\_{2}= \beta v\_{1}+(1-\beta)\theta\_{2} \\\\ v\_{3}= \beta v\_{2}+(1-\beta)\theta\_{3} \\\\ \ldots$

上面的 $θ\_t$ 表示第 $t$ 天的温度，β 是可调节的参数，$V\_t$ 表示 $\frac{1}{1-β}$ 天的每日温度